前景提要

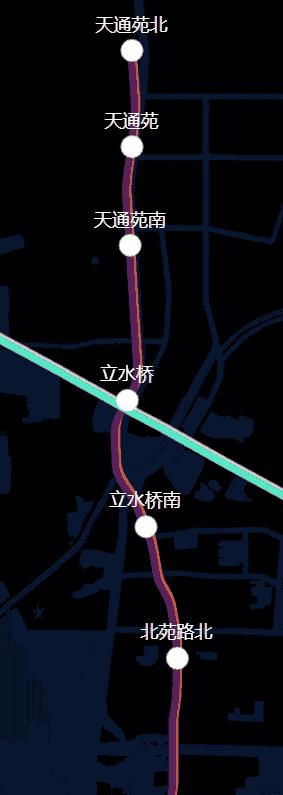
这地铁线，两站之间是有多个坐标点，而后通过高德地图的矢量图形中的折线 Polyline 连接绘制而成。

数据结构大概这样：

[  {    lineName: '地铁5号线',    lineDesc: '天通苑北--宋家庄',    between: ['立水桥', '立水桥南'],    geo: {      type: 'LineString',      coordinates: [        [116.41235270182301, 40.053034125435],        [116.41181287977497, 40.052307128907],        [116.411436903212, 40.051736111112],        [116.41123779296902, 40.051346299914],        [116.41105767144097, 40.050823296441],        [116.41097791883703, 40.050178222657],        [116.41101155599, 40.049252115886],        [116.41106743706598, 40.048259819879],        [116.411084255643, 40.047800021702],        [116.41112630208397, 40.047322862414],        [116.41122531467101, 40.046961805556],        [116.41138020833398, 40.04660780165],        [116.411636013455, 40.046165907119],        [116.41221381293497, 40.045462510851],        [116.41300347222301, 40.044577365452],        [116.413713921441, 40.043393283421],        [116.41419460720499, 40.0425],        [116.41449951171899, 40.041958007813],      ],    },    sectionFlow: 315501,    fullLoad: 7.303263888888889,  },  {    lineName: '地铁5号线',    lineDesc: '天通苑北--宋家庄',    between: ['立水桥南', '北苑路北'],    geo: {      type: 'LineString',      coordinates: [        [116.41449951171899, 40.041958007813],        [116.41480523003497, 40.041415744358],        [116.41497395833403, 40.041099717882],        [116.415112033421, 40.040753851997],        [116.415401746962, 40.039691569011],        [116.41576144748302, 40.038043619792],        [116.41587429470502, 40.037611219619],        [116.41599636501803, 40.037317165799],        [116.41624701605997, 40.036893174914],        [116.416941460504, 40.035935058594],        [116.417190483941, 40.035536838108],        [116.41732720269101, 40.03516764323],        [116.417453070747, 40.034738769532],        [116.41773491753497, 40.03354546441],        [116.41800130208401, 40.032287326389],        [116.41807942708397, 40.031751302084],        [116.41809407552103, 40.03104031033],        [116.41809407552103, 40.030439181858],      ],    },    sectionFlow: 371616,    fullLoad: 8.602222222222222,  },];

根据需求，最后完成后绘制的样子如下图，这是用多边形 Polygon 画的。

问题点

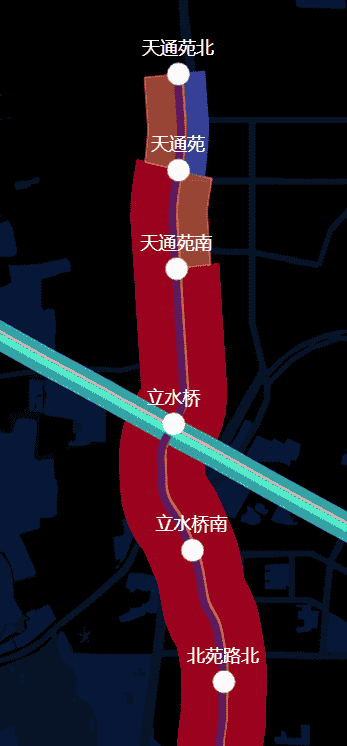
想要绘制完成如上图的关键问题点是：
如何通过已知的一条线，得知距离这条线 N 米的另一条线的坐标呢？

假如正好是纵向的线，那只需加减 x 坐标即可得另一条线的坐标。或者横向的线，那只需加减 y 坐标即可得另一条线的坐标。
那假如是斜着的线，那我该怎样知道应该加减 x 和 y 分别是多少呢？

请留步，思考下思路是怎样样的，我当初是反应了好久才反应过来。

关键的处理点

let path = [];for (let i = 1, length = geo.coordinates.length; i < length; i++) {  let p = geo.coordinates;  let tanX = Math.abs(p[i][0] - p[i - 1][0]),    tantY = Math.abs(p[i][1] - p[i - 1][1]),    angle = Math.atan(tantY / tanX),    moveX = Math.abs(Math.sin(angle)),    moveY = Math.abs(Math.cos(angle));  // 右侧(坐标点顺序，从上往下，从左往右时)  if (direction === "right") {    if (p[i][0] - p[i - 1][0] > 0) {      moveY = -moveY;    }    if (p[i][1] - p[i - 1][1] < 0) {      moveX = -moveX;    }    if (i === 1) {      moveXYs.push({ moveX, moveY });      path.push(p[i - 1]);      path.unshift([p[i - 1][0] + moveX, p[i - 1][1] + moveY]);    }    path.unshift([p[i][0] + moveX, p[i][1] + moveY]);  } else {    if (p[i][0] - p[i - 1][0] < 0) {      moveY = -moveY;    }    if (p[i][1] - p[i - 1][1] > 0) {      moveX = -moveX;    }    if (i === 1) {      moveXYs.push({ moveX, moveY });      path.push(p[i - 1]);      path.unshift([p[i - 1][0] + moveX, p[i - 1][1] + moveY]);    }    path.unshift([p[i][0] + moveX, p[i][1] + moveY]);  }  path.push(p[i]);}

其实想到勾股定理，一切就会迎刃而解。

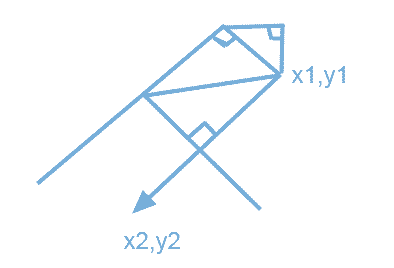
为了清晰一点，我画了个图，而后就不多讲了，就是个简单数学题~

关键代码就是上面，为了保障生成的坐标点在一侧，里面就还需要判断下是向线是左下方斜还是右下方斜。
最后就生成了 Polygon 需要的坐标数组了。

最后

由于工作太久，渐渐的忘却曾经的数学知识，不知道有多少人会和我一样，没有第一时间反应过来，这其实就是个简单的数学题。
想到勾股定理，花费了蛮多时间，随之而来的三角函数知识自然而然的恢复记忆，一切就迎刃而解了。