

在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中能否含有该整数。
例如:下方的二维数组就是每行、每列都递增排序。假如在这个数组中查找数字7,则返回true;假如查找数字5,因为数组中不含有该数字,则返回false。
1 2 8 92 4 9 124 7 10 136 8 11 15最简单粗暴的方式,依次遍历数组中各个元素就可。
function findInMatrixExhaustive(matrix: number[][], target: number): boolean { for (let rowIndex = 0; rowIndex < matrix.length; rowIndex++) { for (let colIndex = 0; colIndex < matrix[rowIndex].length; colIndex++) { const current = matrix[rowIndex][colIndex]; if (current === target) { return true; } } } return false;}此种方式可以算是第一种方法的变体,但利用现有API可以肯定程度上精简代码
function findInMatrixWithApi(matrix: number[][], target: number): boolean { return matrix.flatMap(item => item).includes(target);}此种方式在时间复杂度上会优于前2种方式,利用行和列索引的移动来逐渐查找目标值。
通过题干给出的信息,我们可以得知行和列都保持有序,筛选矩阵中任一元素(element)与目标值(target)进行比照,会出现以下三种情况:
element > target,则目标值可能出现的位置肯定在element的左侧和上方;element < target,则目标值可能出现的位置肯定在element的右侧和下方;element = target,则说明命中目标值。 target-element.png
target-element.png通过上面的辅助图我们可以看到target可能出现的地方出现了重叠,那么有没有什么方法对这种情况进行简化呢?
我们尝试把element移动到矩阵的右上角,这时候你会发现,重叠的部分消失了!
 target-element-no-overlap.png
target-element-no-overlap.png此时,element与target的关系被简化为以下情况:
element>target,则target肯定出现在element的左侧;element<target,则target肯定出现在element的下方;element=target,则说明命中目标值。我们将上述的方法带入到例题中,会得到如下过程:
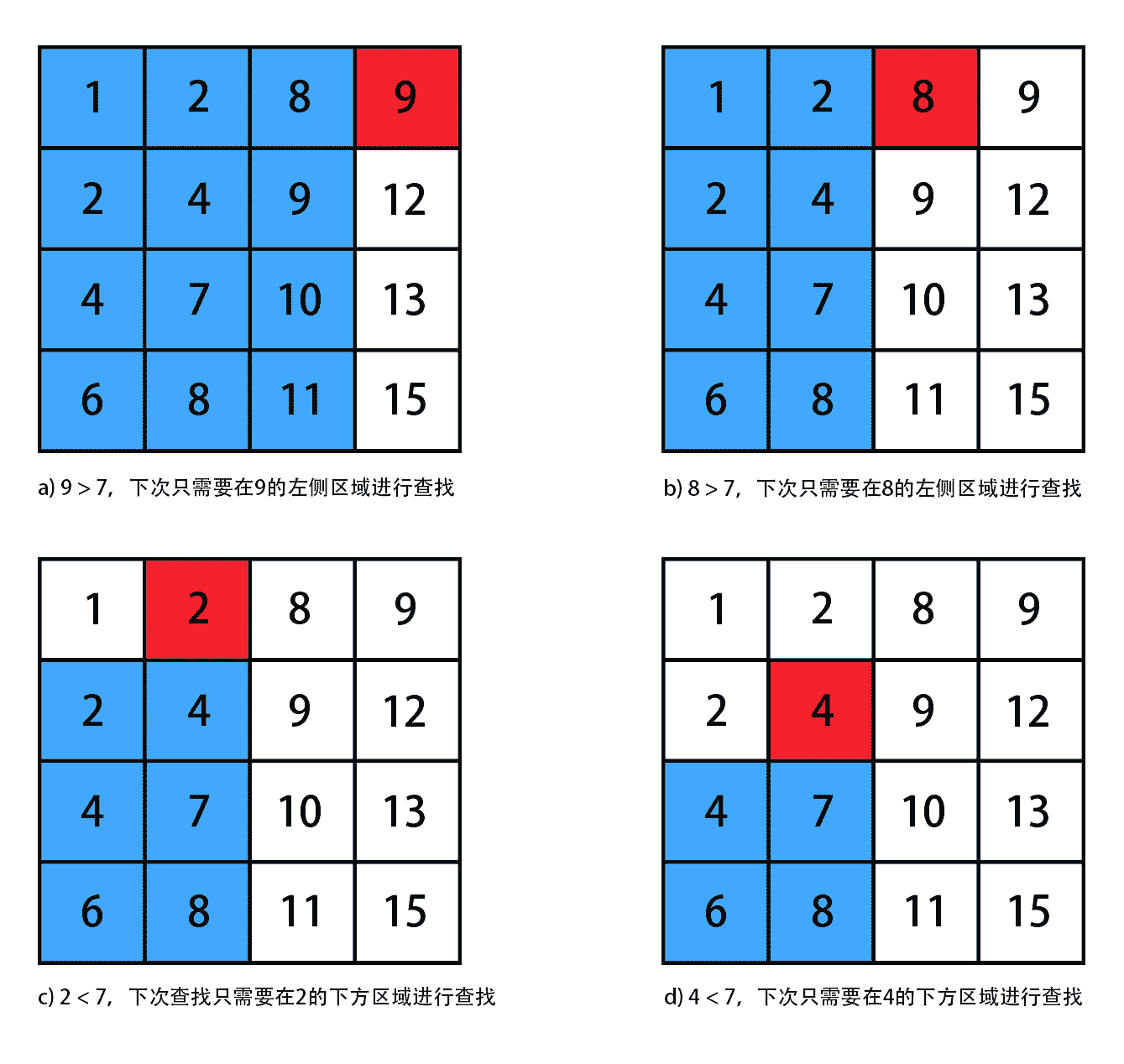 target-element-result.png
target-element-result.png最终,我们匹配到了相应元素,匹配成功。
在匹配过程中,若行索引超出最大行数或者列索引小于0,则说明整个矩阵中未包含目标元素,匹配失败。
function findInMatrix(matrix: number[][], target: number): boolean { const rowSize = matrix.length; const columnSize = matrix[0].length; if (rowSize === 0) { return false; } let row = 0; let col = columnSize - 1; while (row < rowSize && col >= 0) { const current = matrix[row][col]; if (current === target) { return true; } if (current > target) { --col; } else { ++row; } } return false;}