

分类问题和回归问题是监督学习的两大种类:
神经网络模型的效果及优化的目标是通过损失函数来定义的。回归问题处理的是对具体数值的预测。比方房价预测、销量预测等都是回归问题。这些问题需要预测的不是一个事前定义好的类别,而是一个任意实数。处理回顾问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。
交叉熵一般与one-hot和softmax在一起使用。
在分类问题中,one-hot编码是目标类别的表达方式。目标类别需要由文字标签,转换为one-hot编码的标签。one-hot向量,在目标类别的索引位置是1,在其余位置是0。类别的数量就是one-hot向量的维度。在one-hot编码中,假设类别变量之间相互独立。同时,在多分类问题中,one-hot与softmax组合使用。
import numpy as npdef prp_2_oh_array(arr): """ 概率矩阵转换为OH矩阵 arr = np.array([[0.1, 0.5, 0.4], [0.2, 0.1, 0.6]]) :param arr: 概率矩阵 :return: OH矩阵 """ arr_size = arr.shape[1] # 类别数 arr_max = np.argmax(arr, axis=1) # 最大值位置 oh_arr = np.eye(arr_size)[arr_max] # OH矩阵 return oh_arrsoftmax使得神经网络的多个输出值的总和为1,softmax的输出值就是概率分布,应用于多分类问题。softmax也属于激活函数。softmax、one-hot和cross-entropy,一般组合使用。
softmax probabilities + one-hot encoding + cross entropy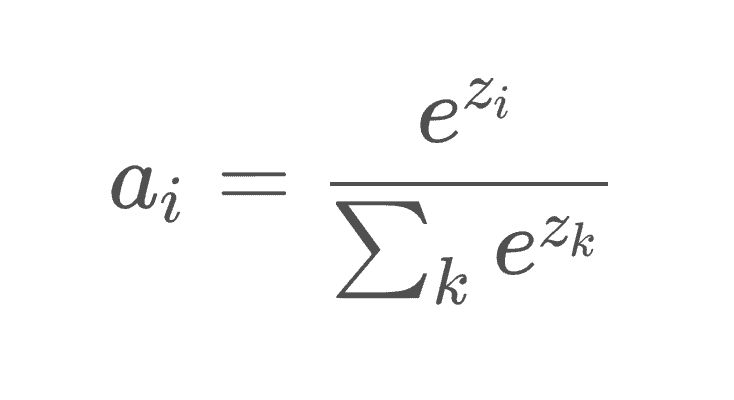 公式
公式交叉熵(cross entropy)比较softmax输出和one-hot编码之间的距离,即模型的输出和真值。交叉熵是一个损失函数,错误值需要被优化至最小。神经网络预计输入数据在各个类别中的概率。最大的概率需要是正确的标签。
常见的损失函数:
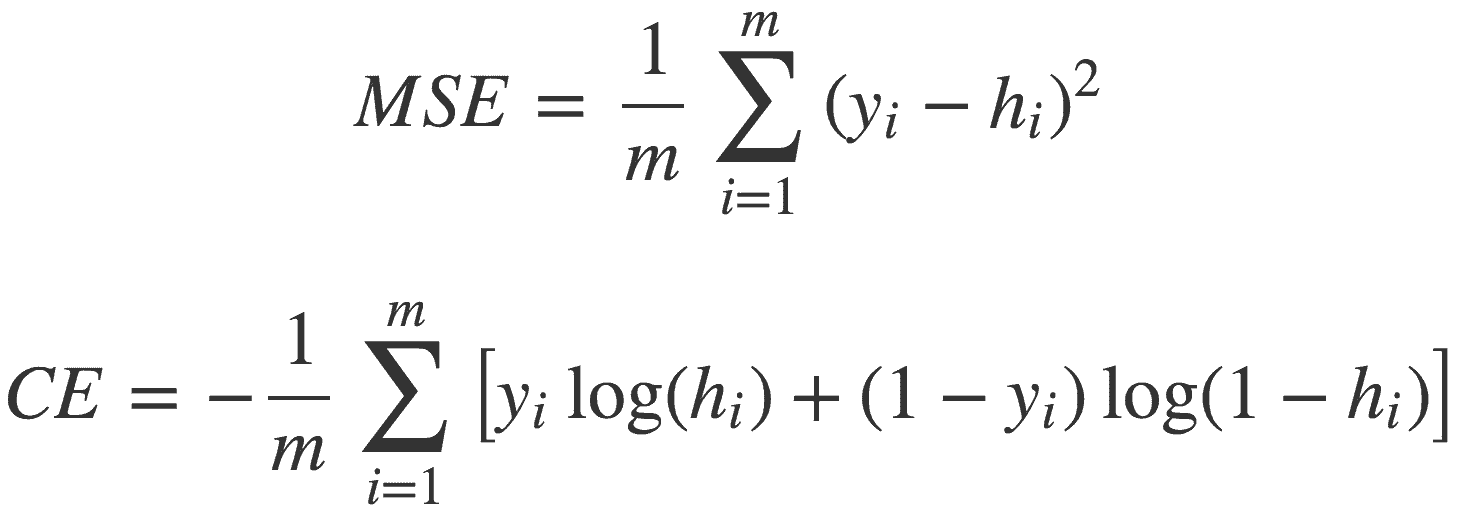 公式
公式其中,y是真值,h是预测值。
softmax和交叉熵的推导,参考:
 推导
推导C是交叉熵,z是wx+b,再对w求导,根据链式法则,w的导数值,就是C的导数乘以w的导数。
(1) MSE+softmax所输出的曲线是波动的,有很多局部的极值点,即非凸优化问题(non-convex),参考:
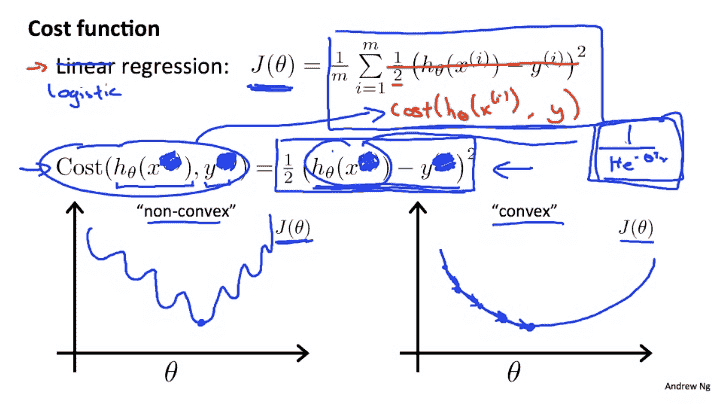 优化曲线
优化曲线(2) 对于正确分类的数据点,CE梯度有一项趋近0,MSE中有两项趋近于0,也就是MSE的梯度消失速度是CE的平方;参考
 正确分类
正确分类(3) 代理商损失函数(surrogate loss function),参考,精确率(accuray)是不连续的,所以需要用连续的函数来代理商,而优化MSE,并不能优化模型的精确度。
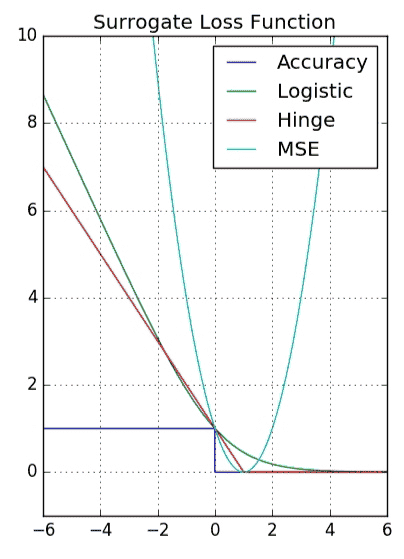 代理商损失函数
代理商损失函数最小二乘是在欧氏距离为误差度量的情况下,由系数矩阵所张成的向量空间内对于观测向量的最佳逼近点。
用欧式距离作为误差度量的起因:
MSE的缺点:
参考1、参考2、参考3